我是来帮加藤大佬写题解的……全世界都没找到加藤大佬写法的说明……很难受……
首先我们把\(p\)看成\(1\)，\(j\)看成\(-1\)，一个区间满足条件就意味着这个区间的所有前缀和都大于等于\(0\)，所有后缀和都大于等于\(0\)
我们记录一下前缀和，所有前缀和大于等于\(0\)就是\(sum[i]-sum[l-1]\geq 0\)，所有后缀和都大于等于\(0\)就意味着\(sum[n]-sum[i-1]\geq sum[n]-sum[r]\)，即\(sum[i-1]\leq sum[r]\)，然后因为\(sum[r]\geq sum[l-1]\)已经在第一个条件里满足了，所以合起来就是\(sum[i]\geq sum[l-1]\)，\(sum[r]\geq sum[i]\)。用人话说，一个区间满足条件，那么这个区间内的\(sum\)都不小于\(sum[l-1]\)且\(sum[r]\)是这个区间中最大的数
于是我们定义\(to[i]\)，意思是\([i,to[i]]\)中的所有数都大于等于\(sum[i]\)，且\(sum[to[i]]\)为这个区间中最大的数，\(to[i]\)为所有满足条件的数中最靠右的。那么我们就可以枚举左端点\(i\)，如果\(s[i]==j\)这个左端点肯定不行，否则这个左端点能匹配的最大的右端点就是\(to[i-1]\)
现在的问题就是怎么求出\(to[i]\)了，我们一开始先把所有的\(to[i]\)都赋值为\(i\)，这样到时候可以少讨论一些边界情况。
首先，如果\(sum[i+1]<sum[i]\)，即\(s[i+1]\)为\(p\)，那么\(to[i]\)只能等于\(i\)，因为它的下一个就小于它了。所以我们只考虑讨论\(s[i+1]\)为\(j\)的情况
我们考虑从后往前做，定义\(nxt[i]\)为它后面的第一个与它\(sum\)相等的位置，记录一个指针\(las\)，表示每一次的\(to[i]\)，现在做到了\(i\)，那么\(las\)应该是指在\(to[i+1]\)的位置。
那么转移会有两种情况
1.\(to[i]=to[i+1]\)，那么直接转移即可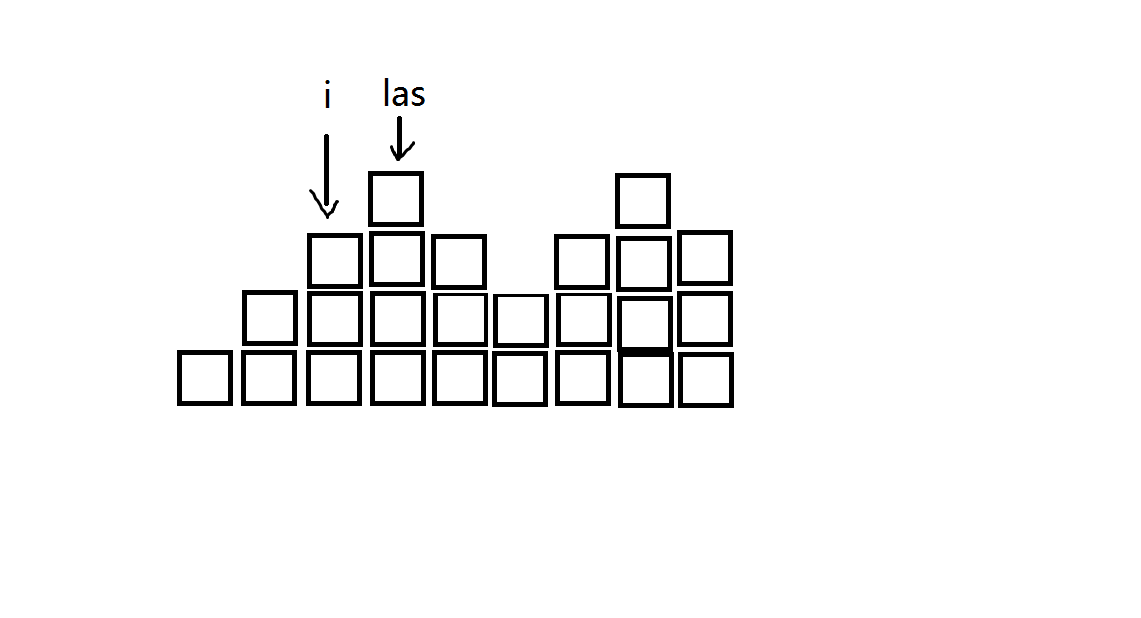
2.\(to[i]\)变大。比如图中，\(k\)的位置才是\(to[i]\)
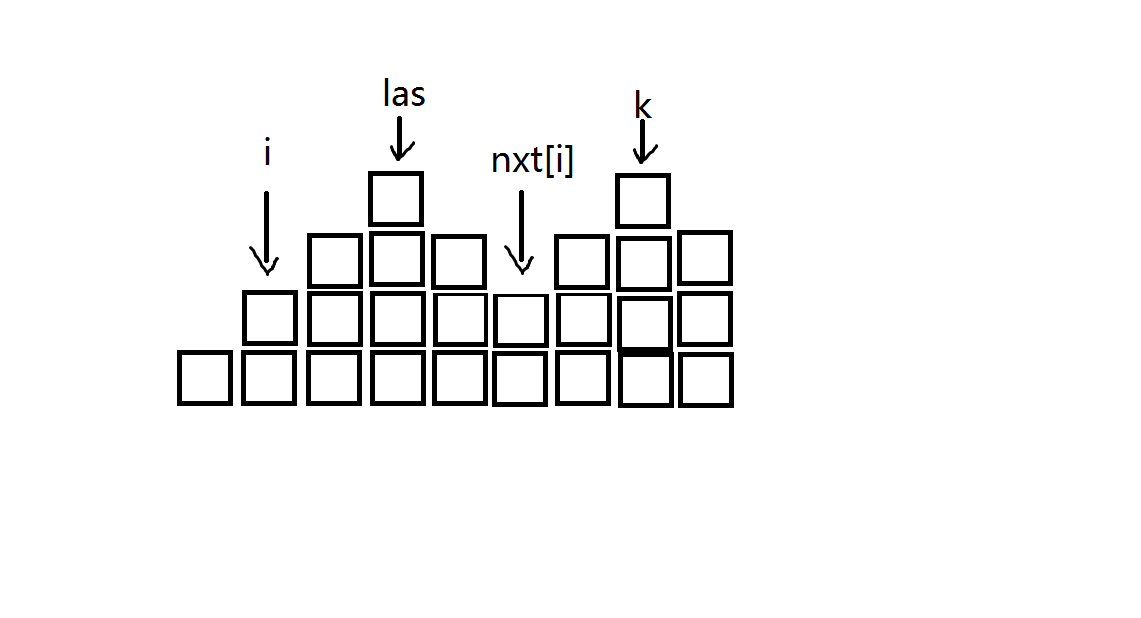我们发现，在本题中，相邻两个数的值最多只会相差\(1\)，于是若是存在如图\(2\)的情况，那么必然存在\(nxt[i]\)。不难证明\([i+1,nxt[i]-1]\)区间内的数肯定同时大于\(sum[i]\)或同时小于\(sum[i]\)，如果全都小于那么有\(sum[i+1]<sum[i]\)，我们之前已经处理掉了。所以\([i+1,nxt[i]-1]\)之间的数必然全都大于\(sum[i]\)。因为\(to[nxt[i]]\)已经求出来了，如果\(sum[to[nxt[i]]]\geq sum[las]\)，我们可以把\([i,nxt[i]-1]\)这一段给接上去，那么新的区间\([i,to[nxt[i]]]\)肯定还是满足条件的，且不难证明不存在比它更优的。这种情况下我们让\(las\)指向\(to[nxt[i]]\)并更新\(to[i]\)即可。 只要处理出\([0,n-1]\)的所有的\(to[i]\)就可以了，最后的答案就是\(max\{to[i-1]-i+1\}(s[i]==p)\)，时间复杂度\(O(n)\)
// luogu-judger-enable-o2//minamoto#includeusing namespace std;const int N=1e6+10;int n,sum[N],head[N],nxt[N],to[N],mn;char s[N];int main(){// freopen("testdata.in","r",stdin); memset(head,-1,sizeof(head)); scanf("%d%s",&n,s+1); for(int i=1;i<=n;++i)sum[i]=sum[i-1]+(s[i]=='p'?1:-1),mn=min(mn,sum[i]); for(int i=n;~i;--i) nxt[i]=head[sum[i]-mn],head[sum[i]-mn]=i,to[i]=i; int ans=0; for(int i=n,las=n;i;--i){ if(s[i]=='j')las=i-1; else{ if(nxt[i-1]>=0&&sum[to[nxt[i-1]]]>=sum[las])las=to[nxt[i-1]]; to[i-1]=las,ans=max(ans,las-i+1); } } printf("%d\n",ans);return 0;}